3.Těleso pohybující se po nakloněné rovině nahoru.

V této kapitole se budeme zabývat pohybem tělesa, které se pohybuje po nakloněné rovině nahoru. Tento pohyb je pouze zdáním, protože, jak víme, každá soustava má tendenci přecházet do stavu s minimální energií. Touto úlohou můžeme ukázat, že při prvním pohledu na věc není vždy zřejmé, proč se daná soustava chová “jaksi podivně”.

Naše soustava se skládá z nakloněné roviny, kterou tvoří dvě rozbíhající se kolejnice, a na nich umístěného dvojkuželu (tj. dvou kuželů stejných rozměrů slepených k sobě podstavami, viz. obr.3.1).

Jestliže tento pokus provedeme, vidíme, že se dvojkužel valí po kolejnicích tak, že se styčné body dvojkužele s kolejnicemi pohybují vzhůru po přímce o stejném sklonu jako je úhel vodorovné roviny s kolejnicemi.

Po proběhnutí děje se bude kužel nacházet v horní části nakloněné roviny (viz. obr.3.2). Obvyklý komentář k tomuto pokusu se omezuje na konstatování, že se nejedná o žádný paradox, neboť těžiště valícího se dvojkužele klesá. Pokusme se však popsat trajektorii těžiště i rotační pohyb dvojkužele.

obr.3.1

obr.3.2

Chceme-li úlohu řešit kvantitativně, musíme sestavit pohybové rovnice dvojkužele a určit vazební podmínku mezi translačním a úhlovým zrychlením. K tomu je třeba najít křivku, po níž se pohybuje těžiště dvojkužele a křivku, kterou vytvoří na kuželi dotykový bod s kolejnicí.

Umístíme souřadnicové osy tak, aby osa x byla orientována po směru pohybu dvojkužele a ležela ve rovině tvořené kolejnicemi, osa y měla směr rotační osy symetrie dvojkužele a osa z měla směr normály k rovině tvořené kolejnicemi. Počátek soustavy souřadnic umístíme do těžiště dvojkužele, právě když leží hroty na kolejnicích.

Stanovení křivky po níž se pohybuje těžiště dvojkužele:

Pro odvození pohybu těžiště použijeme podmínku dotyku kuželové plochy s kolejnicemi (není nutné řešit dotyk s oběma kolejnicemi, stačí vyřešit pouze pro jednu, protože úloha je symetrická).

Souřadnice polohy těžiště označíme:

T = [ x ; 0 ; z ]

Rovnice kuželové plochy:

kde R je poloměr podstavy kužele a h jeho výška. Označme dále tangentu vrcholového úhlu kužele (J je úhel mezi osou kužele a libovolnou povrchovou přímkou).

Po úpravě:

(3.1)

Rovnice přímky reprezentující kolejnici:

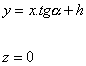(3.2)

kde a je úhel mezi kolejnicí a osou úhlu sevřeného kolejnicemi (viz. obr.3.4).

Společné body, tj. dosazení rovnice přímky do rovnice kuželové plochy:

po úpravě:

(3.3)

Dotyk přímky s kuželovou plochou nastává právě tehdy, je-li diskriminant kvadratické rovnice nulový:

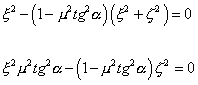(3.3a)

Pak je-li:

a)

(3.4)

Těžiště dvojkužele se pohybuje po přímce.

Znaménko - vyhovuje, v případě + se kužel nachází pod kolejnicí.

b)

V tomto případě vyhovuje rovnici (3.3a) pouze řešení: x = 0 ; z = 0

c)

Rovnici (3.3a) vyhovuje řešení: x = 0 ; z libovolné, z rovnice (3.3) dostáváme z = 0.

Odvodili jsme směrnici přímky, po níž se pohybuje těžiště v souřadnicové soustavě popsané výše, nyní provedeme transformaci souřadnic do soustavy takové, která bude vůči původní pootočena o úhel b , a to tak, že osa x bude ležet ve vodorovné rovině, osa y zůstane v původním směru a osa z se pootočí v rovině xz o úhel b . Touto transformací získáme směrnici přímky, po níž klesá těžiště, vzhledem k vodorovné rovině.

Směrnice přímky v původních souřadnicích je , kde

(3.5)

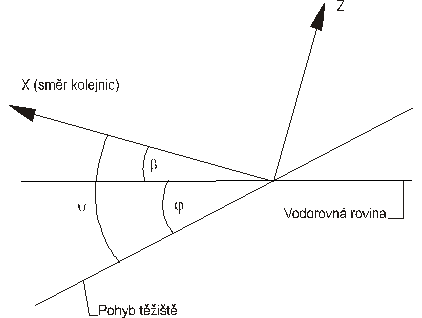
obr. 3.3

Z obr. 3.3 je patrné, že naším úkolem je zjistit tgj , tj. sklon přímky pohybu těžiště vzhledem k vodorovné rovině.

ze součtových vzorců vyplývá:

užitím (3.5) dostaneme:

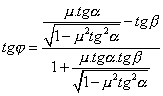
po úpravě:

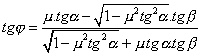(3.6)

Pro realizaci experimentu je nutné zaručit podmínku, aby se těžiště dvojkužele pohybovalo po přímce s negativním sklonem, tj. je nutné, aby odchylka roviny tvořené kolejnicemi vůči vodorovné rovině, byla menší než odchylka přímky pohybu těžiště od vodorovné roviny. Tuto podmínku lze vyjádřit vztahem:

(3.7)

Nyní stanovíme křivku, kterou při pohybu vytvoří na kuželové ploše body jejího dotyku s kolejnicemi. Tato křivka se nazývá zobecněná šroubovice.

Přistoupíme tedy k odvození parametrické rovnice této křivky:

Zajímají nás souřadnice dotykového bodu kolejnice s kuželem.

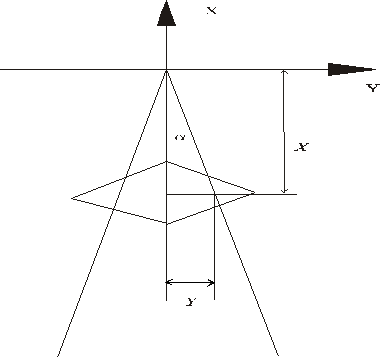
obr.3.4

(3.8)

Vyplývá z podobnosti trojúhelníků:

(3.9)

R - poloměr podstavy kužele

h - výška kužele

r - okamžitý poloměr

f - úhel otočení kužele

Platí:

Po dosazení z (3.8) a (3.9) dostaneme:

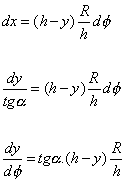
Provedeme substituci:

A získáme diferenciální rovnici prvního řádu se separovatelnými proměnnými:

Po separaci získáme:

Řešením dostáváme obecné řešení:

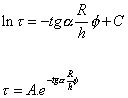
Zpětnou substitucí dostaneme:

Dosazením počátečních podmínek ( f = 0 , y = 0 ) a dosazením za y do (3.9) získáme:

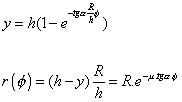(3.10)

Rovnice (3.10) jsou parametrické rovnice křivky (obecné šroubovice na kuželové ploše) v cylindrických souřadnicích, kterou opíše dotykový bod kolejnice s kuželem. Pro námi konkrétně užitý kužel a pro deset otáček vypadá tato křivka takto:

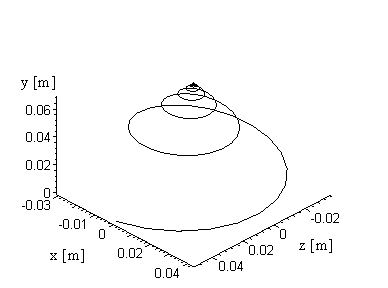
Stanovení vazební podmínky mezi translačním a úhlovým zryhlením:

Jestliže bychom valili po námi užitých kolejnicích válec, pohyboval by se dotykový bod válce a kolejnice po šroubovici vzhledem k pozorovateli spojenému s nerotující těžišťovou soustavou a souvislost mezi translačním a úhlovým zrychlením by byla dána známým vztahem:

My ovšem valíme po kolejnicích dvojkužel, proto musíme vazební podmínku mezi úhlovým zrychlením a zrychlením těžiště dvojkužele elementárně odvodit. Předpokládáme, že se dvojkužel valí bez prokluzu.

Nyní se opět vracíme do souřadnicové soustavy používané na začátku článku, protože bude pro naše následující výpočty jednodušší.

Má-li kvadratická rovnice (3.3) pouze jediné řešení, pak bod dotyku má souřadnice:

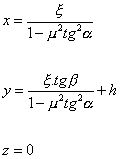(3.11)

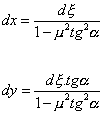(3.12)

Elementární dráhu uraženou těžištěm dl lze vyjádřit pomocí (3.4):

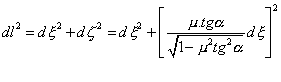
(3.13)

Odpovídající elementární posunutí bodu dotyku ds po kolejnici lze vyjádřit pomocí (3.12):

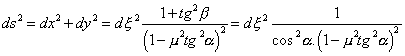
Použitím vztahu (3.13) dostaneme:

(3.14)

Je zřejmé, že:

(3.15)

translační rychlost těžiště (3.16)

úhlová rychlost rotace dvojkužele (3.17)

Srovnáním vztahů (3.14) , (3.15) a dosazením ze vztahů (3.16) , (3.17) získáme vazební podmínku pro rychlost těžiště a úhlovou rychlost rotace dvojkužele:

(3.18)

Derivováním vztahu (3.18) dostaneme vazební podmínku pro zrychlení těžiště a úhlové zrychlení rotace dvojkužele:

(3.19)

Po dosazení rovnic (3.10) do vztahů (3.18) a (3.19) dostaneme vazební podmínky jako funkce úhlu otočení dvojkužele f :

(3.20)

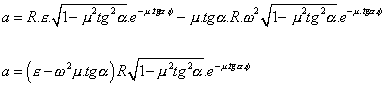(3.21)

Stanovili jsme vazební podmínky (3.20) a (3.21) a můžeme tedy přistoupit k popisu pohybu dvojkužele.

Nejprve pro ilustraci vyjádříme úhlovou a translační rychlost v závislosti na f . K tomuto použijeme energetické úvahy, a to konkrétně zákon zachování mechanické energie.

Jednotlivé příspěvky mechanické energie, které připadají v našem případě v úvahu jsou: tíhová potenciální energie, translační kinetická energie a rotační kinetická energie. Můžeme tedy zákon zachování mechanické energie zapsat ve tvaru:

(3.22)

w - značí okamžitou výšku těžiště nad nulovou hladinou potenciální energie.

Nulovou hladinu tíhové potenciální energie umístíme na úroveň těžiště na počátku experimentu, tj. v okamžiku, kdy f = 0, v = 0, w = 0. Pak E = 0.

Ve vztahu (3.22) vystupují jako neznámé translační rychlost v a úhlová rychlost w , jednu však můžeme vyjádřit pomocí druhé z podmínky (3.20). Nyní můžeme tedy napsat rovnici pro jednu neznámou w :

(3.23)

Vytknutím w z prvních dvou členů a převedením výrazu pro potenciální energii dostaneme:

(3.24)

Pro přehlednost označme výraz jako A (současně je )

Rovnici (3.24) přepíšeme do tvaru:

(3.25)

Abychom mohli dále rovnici (3.25) upravit, je nutné vypočíst moment setrvačnosti dvojkužele. Moment setrvačnosti rotačního tělesa vytvořeného rotací plochy křivočarého lichoběžníka ohraničeného obloukem čáry , je:

kde r je hustota materiálu dvojkužele.

V našem případě je pro jednu polovinu dvojkužele, tj:

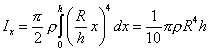(3.26)

Moment setrvačnosti jsme určili pouze pro polovinu dvojkužele, proto pro celý dvojkužel bude jeho hodnota dvojnásobná, tj: .

Vyjádříme I_x ve tvaru:

(3.27)

Toto dosáhneme jestliže vyjádříme hmotnost kužele ve vztahu (3.27) a porovnáme ze vztahem (3.26). Takto získáme vyjádření pro moment setrvačnosti dvojkužele:

(3.28)

Dosadíme-li do vztahu (3.25) dostaneme:

Celou rovnici vydělíme m , vynásobíme 2 a použijeme vztah (3.18):

(3.29)

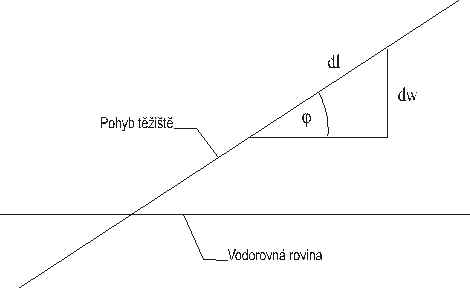
Pro konečné vyjádření úhlové rychlosti w jako funkce úhlu otočení f nám zbývá vyjádřit pouze okamžitou výšku w těžiště dvojkužele nad nulovou hladinou potenciální energie.

obr.3.5

Z obr. 3.5 je vidět, že:

(3.30)

Porovnáním vztahů (3.14) a (3.15) získáme výraz pro dl a po dosazení do vztahu (3.30) dostaneme:

Za r dosadíme ze vztahu (3.10):

(3.31)

Funkci w získáme integrací výrazu (3.31) v mezích od f =0 do f a po zpětném dosazení r ze vztahu (3.10) dostaneme:

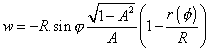(3.32)

Vztah (3.32) dosadíme do rovnice (3.29):

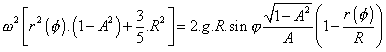
Jednoduchou úpravou získáme vyjádření úhlové rychlosti w jako funkce úhlu otočení f dvojkužele:

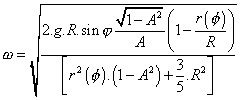(3.33)

kde

Abychom získali vyjádření translační rychlosti těžiště dvojkužele stačí použít vztahy (3.18) a (3.33):

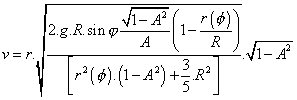(3.34)

Do této chvíle jsme pracovali s naprosto obecným dvojkuželem a obecnou nakloněnou rovinou sestavenou se stoupajících a rozbíhajících se kolejnic. Jestliže však chceme mít názornou představu o tom, jak se pohybuje skutečný dvojkužel po skutečných kolejnicích, budeme je muset použít i v našich výpočtech. Použitý dvojkužel a kolejnice mají tyto parametry:

R = 3,98 cm

h = 5,50 cm

a = 0,131 rad

b = 0,087 rad

g = 9,81 ms^-2

Jestliže použijeme tyto parametry a vyneseme do grafu závislost úhlové rychlosti w na otočení dvojkužele f o 100 rad, získáme takovouto závislost:

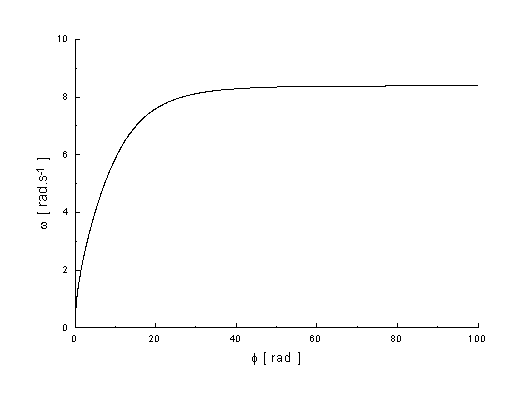
graf.3.1

Vyneseme-li podobně velikost translační rychlosti těžiště, získáme tuto závislost:

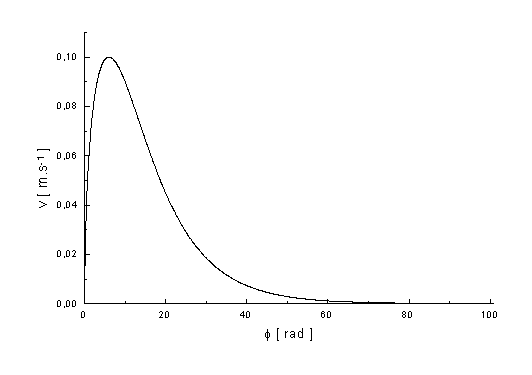
graf.3.2

Na grafu 3.1 je patrné, že hodnota úhlové rychlosti w konverguje pro (tj. dosáhne jí po nekonečném počtu otáček) k určité hodnotě, v našem experimentu je:

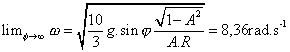
Z grafu 3.2 je velmi dobře vidět, že pro tutéž situaci konverguje hodnota velikosti translační rychlosti těžiště dvojkuželu k hodnotě 0, tj.:

Tyto limitní případy popisují situaci, že se dvojkužel otáčí konstantní úhlovou rychlostí na hrotech a nijak jinak se nepohybuje.

Další zajímavostí v grafu 3.2 je, že hodnota velikosti rychlosti v nabývá v při určité hodnotě úhlu otočení f své maximální hodnoty. Tento jev zcela zřejmý, jestliže si uvědomíme, že na počátku děje je v = 0 a na jeho konci taktéž.

My se nyní budeme zabývat tím, pro jaký úhel f je v maximální:

Podmínka pro maximum funkce:

Vyřešíme-li tuto rovnici vzhledem k f , získáme jedinou reálnou hodnotu:

Pro tuto hodnotu f je velikost translační rychlosti:

Ukázali jsme jak se chovají úhlová a translační rychlost dvojkužele v závislosti na úhlu otočení f .

Nyní sestavíme pohybovou rovnici pro dvojkužel. K tomu však potřebujeme znát všechny síly, které na dvojkužel působí a jejich momenty.

Na dvojkužel budou působit normálové tlakové síly od kolejnic ( a ), síly tření ( a ) a síla tíhová.

V následujícím se budeme věnovat normálovým silám:

Spočteme normály ke kuželové ploše v bodech dotyku dvojkužele s kolejnicemi:

Jestliže je v rovnici (3.3) je nulový diskriminant, pak body dotyku mají souřadnice:

Parametrické rovnice kuželové plochy, na níž leží bod Q₊ jsou (použijeme-li x a z jako parametry a vyjádříme y):

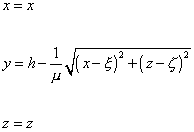
Tečné vektory ke kuželové ploše:

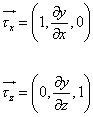
Normála:

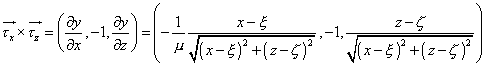
Výpočet jednotkové vnitřní normály v bodě dotyku Q₊, tj. směr síly :

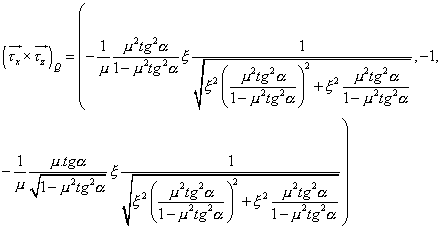
Po úpravě:

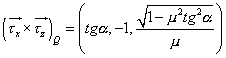(3.35)

Velikost normály:

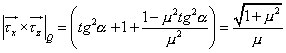
Směry normálových sil a ( a jsou symetrické podle roviny xz):

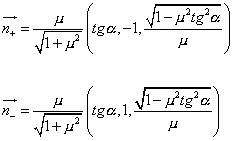(3.36)

Normálové síly:

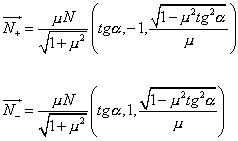(3.37)

Statické třecí síly:

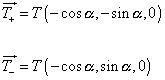(3.38)

Tíhová síla:

Celková působící síla:

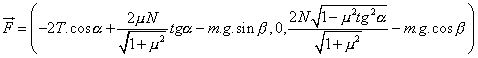(3.39)

Momenty sil vůči těžišti:

souřadnice těžiště:

ramena sil (po úpravě):

Moment síly vůči těžišti:

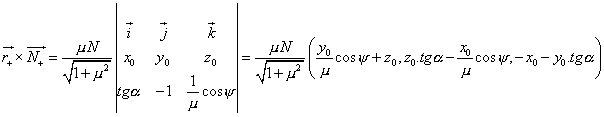
Moment síly vůči těžišti:

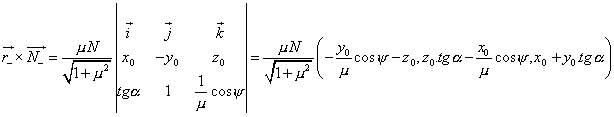
Celkový moment normálových sil vůči těžišti (po dosazení a úpravě):

Celkový moment statických třecích sil vůči těžišti:

Moment tíhové síly vůči těžišti:

Výsledný moment sil vůči těžišti:

(3.40)

Ze vztahů (3.11) a (3.13) dostaneme závislost x-ové souřadnice těžiště na těžištěm uražené vzdálenosti:

(3.41)

Můžeme psát:

(3.42)

(3.43)

Nyní máme vše potřebné, abychom mohli sestavit pohybové rovnice. Matematické pohodlí nás však vede k provedení ještě jedné transformace souřadnic, a to otočení souřadnicové soustavy kolem osy y o úhel y (viz obr.3.6)

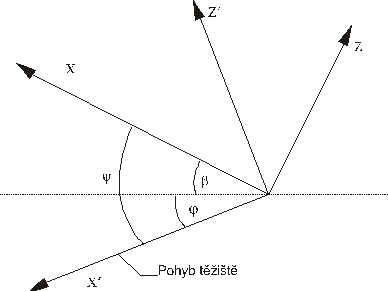
obr.3.6

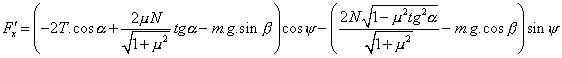
po úpravě:

(3.44)

Z vazební podmínky, tj., že dvojkužel se pohybuje pouze ve směru osy x, vyplývá , tj.

Z předchozího vztahu přímo dostaneme souvislost mezi velikostí normálové a třecí síly:

(3.45)

Nyní můžeme zapsat pohybové rovnice:

(3.46a)

(3.46b)

Z rovnice (3.46b) a pomocí vztahů (3.41) a (3.42) vyjádříme velikost třecí síly T:

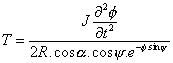(3.47)

Dosazením vztahu (3.47) do rovnice (3.46a) dostaneme:

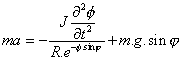(3.48)

Úpravou vztahu (3.48) pomocí výrazu (3.21) získáme nelineární diferenciální rovnici druhého řádu:

Pomocí vztahu (3.28) ještě upravíme na tvar:

(3.49)

Rovnici (3.49) nelze vyřešit analyticky, proto ji budeme řešit numerickými metodami.

Po výpočtu v programu Octave získáme jako výstup tyto grafické závislosti:

Graf závislosti úhlové rychlosti w na úhlu otočení f .

graf.3.3

Graf závislosti translační rychlosti těžiště v na úhlu otočení f .

graf.3.4

Porovnáním grafů 3.1, 3.3 a grafů 3.2, 3.4, je patrné, že řešením rovnice (3.49) jsme dospěli ke stejným výsledkům jako pomocí zákona zachování mechanické energie (3.22).

Řešení rovnice (3.49) nám však umožňuje graficky znázornit i časové závislosti.

Graf závislosti úhlové rychlosti w na čase t.

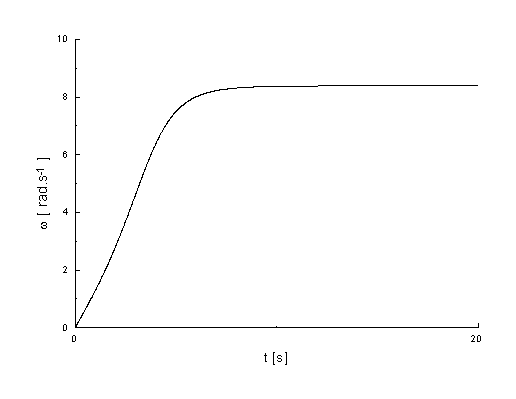
graf.3.5

Graf závislosti translační rychlosti těžiště v na čase t.

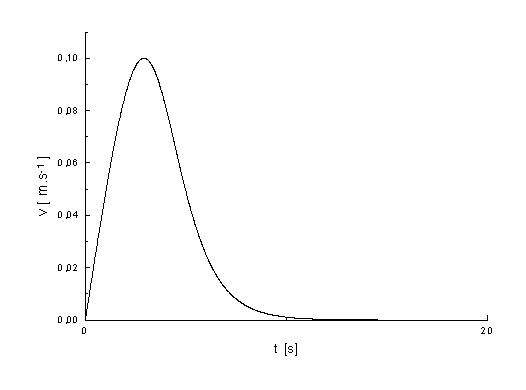
graf.3.6

Na začátku výpočtů jsme předpokládali, že se dvojkužel pohybuje po kolejnicích bez prokluzu. Vztah (3.47) udává velikost třecí síly T a vztah (3.45) velikost normálové síly N. Jestliže se má dvojkužel valit bez prokluzu musí být splněna podmínka:

, (3.50)

kde f_s je koeficient statického tření mezi dvojkuželem a kolejnicemi.

V našem experimentu je dvojkužel ocelový a kolejnice mosazné. Koeficient statického tření mezi těmito dvěma materiály má hodnotu . V našem experimentu k prokluzu nedojde, jak je vidět z grafů 3.7 a 3.8.

Graf závislosti třecí síly na čase.

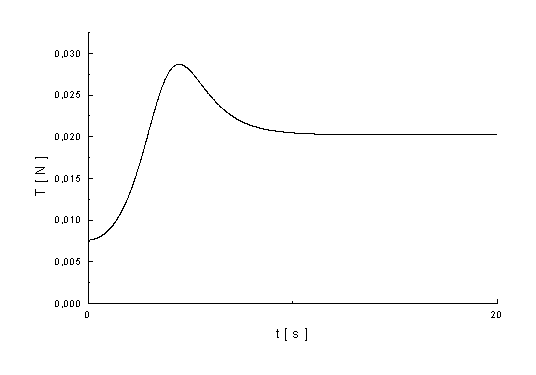
graf.3.7

Graf závislosti normálové síly na čase.

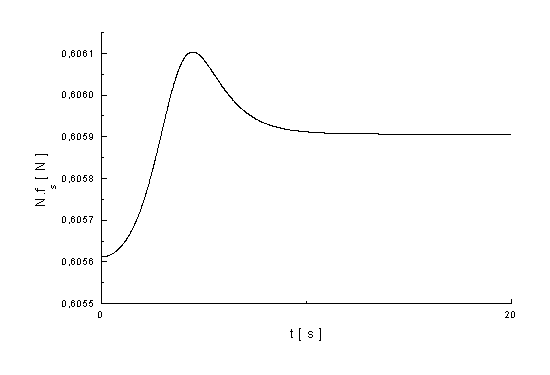
graf.3.8

K prokluzu by mohlo dojít v případě, kdy by koeficient smykového tření mezi dvojkuželem a kolejnicemi byl menší než 0,0095. Na grafu 3.9 vidíme závislost třecí a normálové síly na čase v případě, že koeficient statického tření mezi dvojkuželem a kolejnicemi má hodnotu . Tato situace nemůže v reálném experimentu nastat, protože nejnižší koeficienty statického tření jsou alespoň třikrát větší ( např. ocel na ledu - ).

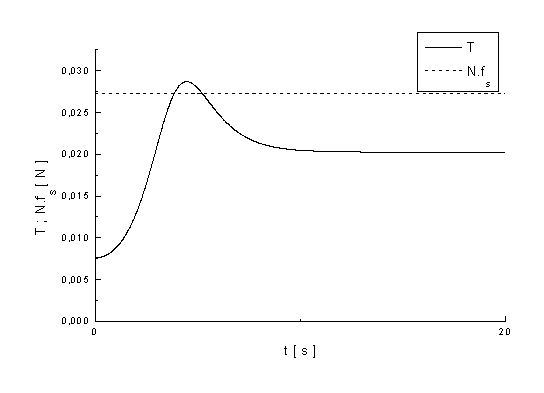
graf.3.9

V našem experimentu se tedy dvojkužel pohybuje v souladu s pohybovými rovnicemi, s tím, že zanedbáváme valivé tření.