Next: Astronomické a fyzikální konstanty, Up: ulohy Previous: ExtragalaktickĂĄ astronomie
Úloha 14.1Pomocí databáze SIMBAD (http://simbad.u-strasbg.fr/simbad/)
nalezněte souřadnice, radiální rychlost a paralaxu a) hvězdy Arcturus, b)
hvězdy HD 37776, c) galaxie M 31.
Řešení: Na stránce http://simbad.u-strasbg.fr/simbad/ zvolíme hledání prostřednictvím názvu ("Query by identifier") a jako "Identifier" zadáme název hvězdy.
Úloha 14.2Na základě dat z článku autorů M. Asplund, N. Grevesse a A. J. Sauval "The
Solar Chemical Composition" (2005, ASP Conference Series, Vol. 336, str. 25)
nakreslete graf relativního zastoupení jednotlivých prvků (vzhledem k vodíku) ve
sluneční atmosféře. Stanovte hmotnostní podíl prvků těžších než helium.
Řešení: Na stránce http://adsabs.harvard.edu zvolíme "Search", "Astronomy and Astrophysics Search", hledáme např. články autora "Asplund" z roku 2005. Vybereme hledaný článek, který je možné získat prostřednictvím stránek xxx.lanl.gov (volba "arXiv e-print"). V Tabulce 1 tohoto článku jsou uvedeny hodnoty relativního zastoupení jednotlivých prvků jako
Úloha 14.3Nalezněte deset nejbližších hvězd viditelných pouhým okem.
Řešení: Na stránkách CDS (http://cds.u-strasbg.fr) zvolíme VizieR, databáze "HIP" (Hipparcos), klepneme na "Find Catalogue", zvolíme "I/239/hip_main", v políčku Vmag vyplníme "<6", zvolíme "Sort" podle políčka "Plx", zvolíme "Output Order" jako "-" a klepneme na "Submit Query" a získáme seznam nejbližších a nejjasnějších hvězd (viz tabulka, ve které je zaneseno prvních deset z nich). Označení bylo získáno pomocí databáze SIMBAD.
| HIP | hvězda |
|
||
| 71681 | 1,35 |
|
||
| 71683 | -0,01 |
|
||
| 32349 | -1,44 |
|
||
| 16537 |
|
3,72 |
|
|
| 104214 | 61 Cyg | 5,20 |
|
|
| 37279 | 0,40 |
|
||
| 108870 |
|
4,69 |
|
|
| 8102 | 3,49 |
|
||
| 19849 | 4,43 |
|
||
| 88601 | 70 Oph | 4,03 |
|
Úloha 14.4V jedné ze svých knih A. C. Clarke píše o tom, že Halleyova kometa má dvě
oddělená jádra. Pomocí databáze NASA ADS (http://adsabs.harvard.edu) ověřte, zda je toto tvrzení hodnověrné.
Řešení: Na stránce http://adsabs.harvard.edu zvolíme vyhledávání ("Search"), "Astronomy and Astrophysics Search" a jako položku "Title Words" zvolíme klíčová slova "Halley comet splitting". Získáme několik odkazů věnujících se rozpadu jádra Halleyovy komety během jejího posledního průchodu kolem Slunce. Tvrzení je jednou z úspěšných předpovědí autora.
Úloha 14.5
Nakreslete křivku vyzařování černého tělesa pro teploty
![]() a
a
![]() . Čím se liší?
. Čím se liší?
Řešení: Pro spektrální hustotu energie vyzařování černého tělesa platí
function b(tep,lam:double):double;
const h=6.6256e-34; {Planckova konstanta}
c=2.99792e8; {rychlost svetla}
bolk=1.38054e-23; {Boltzmannova konstanta}
var lam5:double;
begin
lam5:=lam*lam*lam*lam*lam;
b:=8.0*pi*h*c/lam5/(exp(h*c/lam/bolk/tep)-1.0);
end;
Graf závislosti Planckovy funkce na vlnové délce pro teploty
![]() a
a
![]() je na obrázku 2. Jsou patrné dva závěry.
V celém intervalu vlnových délek platí, že
spektrální hustota vyzařovaná tělesem s vyšší teplotou je větší. Patrný je
posuv maxima obou křivek, pro vyšší teploty směrem k nižším vlnovým
délkám.
je na obrázku 2. Jsou patrné dva závěry.
V celém intervalu vlnových délek platí, že
spektrální hustota vyzařovaná tělesem s vyšší teplotou je větší. Patrný je
posuv maxima obou křivek, pro vyšší teploty směrem k nižším vlnovým
délkám.
Úloha 14.6Pomocí katalogů CDS nalezněte pět nejjasnějších hvězd v rentgenovém oboru,
které mají spektrální typ O nebo B.
Řešení: Na stránce http://cdsweb.u-strasbg.fr zvolíme "VizieR", jako "Wavelength" zvolíme "X-ray", jako "Astronomical keywords" zvolíme "Stars:early-type" a zadáme hledání ("Find Catalogues"). Vybereme katalog odpovídající úloze, "ROSAT all-sky survey catalogue of OB stars", "Detections". V prohledávání zvoleného katalogu zaškrtneme třídění ("Sort") podle pozorované hustoty toku rentgenového záření ("Apparent X-ray flux"). Aby se třídění opravdu provedlo, je nutné ještě zadat vhodnou podmínku ("Constraint", vzhledem k velikosti pozorovaného toku např. "
Úloha 14.7Pomocí atlasu slunečního spektra http://bass2000.obspm.fr/solar_spect.php nakreslete sluneční spektrum
v intervalu vlnových délek
![]() a pokuste se identifikovat
nejsilnější čáry.
a pokuste se identifikovat
nejsilnější čáry.
Řešení: Na uvedené stránce získáme potřebná data. Zdroj pro identifikaci čar nalezneme v katalozích CDS, http://cdsweb.u-strasbg.fr/cats/Cats.htx, zvolíme hledání "identification spectrum", katalog "VI/26 Identification list of lines in Stellar Spectra (Moore, 1959)" a jeho novou verzi "VI/71A Revised version of the ILLSS Catalogue (Coluzzi 1993-1999)", v prohledávání zvoleného katalogu ("VizieR query form") zadáme podmínku pro vlnové délky jako "
Úloha 14.8
S použitím programu STATSTAR vypočtěte model hvězdy
se sluneční hmotností (s parametry1 hmotnost, zářivý výkon a efektivní
teplota rovnými
![]() ,
,
![]() a
a
![]() , chemické složení
odpovídá Slunci,
, chemické složení
odpovídá Slunci, ![]() ,
, ![]() a
a ![]() ).
).
Řešení: Graf jednotlivých závislostí je na obr. 4.
Úloha 14.9
Pomocí programu STATSTAR vypočtěte model hvězdy na hlavní posloupnosti
s hmotností
![]() (pro tuto hvězdu jsou zářivý výkon a efektivní
teplota rovny
(pro tuto hvězdu jsou zářivý výkon a efektivní
teplota rovny
![]() a
a
![]() ) a porovnejte
ho s modelem hvězdy o hmotnosti
) a porovnejte
ho s modelem hvězdy o hmotnosti
![]() (pro tuto hvězdu jsou
zářivý výkon a efektivní teplota rovny
(pro tuto hvězdu jsou
zářivý výkon a efektivní teplota rovny
![]() a
a
![]() ).
Pro obě hvězdy předpokládejte chemické složení odpovídající Slunci
(
).
Pro obě hvězdy předpokládejte chemické složení odpovídající Slunci
(![]() ,
, ![]() a
a ![]() ).
).
Řešení: Centrální tlak a teplota hvězdy se sluneční hmotností (
Úloha 14.10
Porovnejte parametry hvězd s hmotností
![]() s různými chemickými
složeními
s různými chemickými
složeními ![]() ,
, ![]() ,
, ![]() a
a ![]() ,
, ![]() ,
, ![]() .
Vysvětlete případné rozdíly.
.
Vysvětlete případné rozdíly.
Řešení: Hvězda s vyšším obsahem kovů má nižší efektivní teplotu (
Úloha 14.11
Pomocí programu STATSTAR vypočtěte teoretickou hlavní posloupnost pro hvězdy
s hmotnostmi
![]() -
-
![]() . Zvolte sluneční chemické
složení (
. Zvolte sluneční chemické
složení (![]() ,
, ![]() a
a ![]() ).
).
Řešení: Charakteristiky2hvězd hlavní posloupnosti získané programem STATSTAR jsou uvedeny v tabulce.
|
|
||
Úloha 14.12Podle dat z článku Allende Prieto C., Lambert D. L., Astronomy &
Astrophysics 352, 555, dostupných v databázi CDS http://cdsweb.u-strasbg.fr nakreslete HR diagram nejbližších hvězd
nacházejících se do vzdálenosti
![]() .
.
Řešení: Na uvedené stránce zvolíme např. "Catalogues ", hledání podle "Allende Prieto Lambert", zvolíme hledaný článek a získáme potřebný soubor (např. zvolíme stahování prostřednictvím http, soubor "table1.dat.gz". Formát souboru je popsán v popisu katalogu. Pomocí získaného souboru nakreslíme HR diagram (obrázek 5).
Úloha 14.13Nakreslete vývojový HR diagram. Potřebné soubory získejte na stránkách CDS
http://cdsweb.u-strasbg.fr z článku Schaller G. a kol., Astronomy &
Astrophysics Suppl. Ser. 96, 269. S pomocí nakresleného grafu odhadněte hmotnost
hvězdy ![]() Ori E, pro kterou byla z pozorování zjištěna efektivní teplota
Ori E, pro kterou byla z pozorování zjištěna efektivní teplota
![]() a poloměr
a poloměr
![]() .
.
Řešení: Na uvedené stránce zvolíme např. "Catalogues ", hledání podle "Schaller" a zvolíme hledaný článek. Například prostřednictvím http získáme potřebné soubory "table*" a nakreslíme graf 6. Odhadovaná hmotnost hvězdy
Úloha 14.14
Nakreslete graf závislosti poměru koncentrace neutrálního vodíku k celkové
koncentraci vodíku v závislosti na teplotě za předpokladu termodynamické
rovnováhy. Pro zjednodušení předpokládejte, že koncentrace
elektronů je
![]() .
.
Řešení: Pro Sahovo rozdělení platí
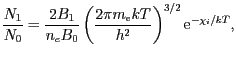
program sahav;
var tep,nel,x:double;
i:integer;
function saha(tep,nel:double):double;
const em=9.10956e-31; {hmotnost elektronu}
bolk=1.38054e-23; {Boltzmannova konstanta}
h=6.6256e-34; {Planckova konstanta}
exc=13.598; {excitacni energie H v eV}
enab=1.6022e-19; {naboj elektronu}
var b1,b2,x:double;
begin
b1:=2.0;
b2:=1.0;
x:=2.0*pi*em*bolk*tep/h/h;
saha:=2.0*b2*sqrt(x)*x*exp(-exc*enab/bolk/tep)/nel/b1;
end;
begin
tep:=1000;
nel:=1.0e17;
for i:=1 to 200 do
begin
tep:=tep+100.0;
x:=saha(tep,nel);
writeln(tep,1.0/(1.0+x));
end;
end.
Výsledný graf je na obrázku 7.
Úloha 14.15
Nakreslete graf závislosti poměru koncentrace vodíku s elektronem, nacházejícím
se na druhé energetické hladině k celkové koncentraci vodíku v závislosti na
teplotě za předpokladu termodynamické
rovnováhy. Pro zjednodušení předpokládejte, že koncentrace
elektronů je
![]() . Vysvětlete tvar získaného grafu.
Jaký závěr lze učinit pro čáry Balmerovy série vodíku?
. Vysvětlete tvar získaného grafu.
Jaký závěr lze učinit pro čáry Balmerovy série vodíku?
Řešení: Využijeme výsledku předcházejícího příkladu (14) pro výpočet relativního zastoupení neutrálního vodíku. Pro výpočet podílu koncentrace vodíku na druhé hladině k celkovému množství neutrálního vodíku využijeme Boltzmannovy rovnice
Pro získání grafu na obrázku 8 je možné použít následující program,
program sahav2;
const em=9.10956e-31; {hmotnost elektronu}
bolk=1.38054e-23; {Boltzmannova konstanta}
h=6.6256e-34; {Planckova konstanta}
exc=13.598; {excitacni energie H v~eV}
enab=1.6022e-19; {naboj elektronu}
var tep,nel,x,n,gh,g2,x2:double;
i:integer;
function saha(tep,nel:double):double;
const em=9.10956e-31; {hmotnost elektronu}
bolk=1.38054e-23; {Boltzmannova konstanta}
h=6.6256e-34; {Planckova konstanta}
exc=13.598; {excitacni energie H v~eV}
enab=1.6022e-19; {naboj elektronu}
var g1,g2,x:double;
begin
g1:=2.0;
g2:=1.0;
x:=2.0*pi*em*bolk*tep/h/h;
saha:=2.0*g2*sqrt(x)*x*exp(-exc*enab/bolk/tep)/nel/g1;
end;
begin
tep:=1000;
nel:=1.0e20;
gh:=2.0;
n:=2.0;
g2:=2.0*n*n;
for i:=1 to 200 do
begin
tep:=tep+100.0;
x:=saha(tep,nel);
x2:=g2/gh*exp(-exc*enab/bolk/tep*(1.0-1.0/n/n));
writeln(tep,x2/(1.0+x));
end;
end.
ve kterém jsme využili funkci saha z předcházejícího příkladu.
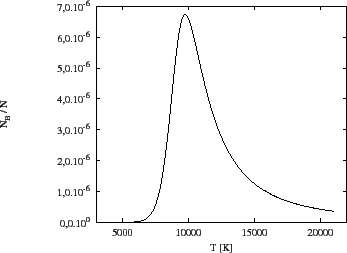
|
Tvar křivky je dán jednak tím, že s rostoucí teplotou roste podíl excitovaných atomů vodíku k atomům v základním stavu. Proto křivka pro nízké teploty zprvu roste. Pro vyšší teploty se začíná vodík ionizovat, ubývá celkového množství atomů vodíku v základním stavu a tedy i podíl atomů vodíku na druhé hladině klesá.
Balmerovy čáry vznikají přechody mezi hladinou s kvantovým číslem ![]() a
vyššími hladinami. Proto jsou za dané elektronové koncentrace nejvýraznější
právě pro teplotu
a
vyššími hladinami. Proto jsou za dané elektronové koncentrace nejvýraznější
právě pro teplotu
![]() .
.
Úloha 14.16
Intenzita vycházející z izotermické vrstvy nacházející se v lokální
termodynamické rovnováze je dána přesným řešením rovnice přenosu záření
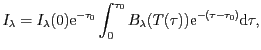
Řešení: Pro výpočet závislosti vystupující intenzity na tloušťce vrstvy je možné použít následující program:
program izotv;
var i: integer;
b,tau,int,i0: double;
begin
b:=2.0;
i0:=3.0;
for i:=1 to 100 do
begin
tau:=(i-1)/10.0;
int:=i0*exp(-tau)+b*(1.0-exp(-tau));
writeln(tau,int);
end;
end.
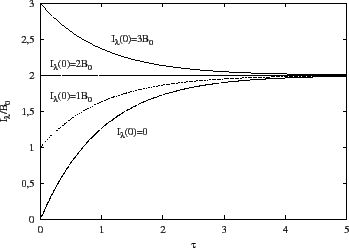
|
Úloha 14.17
Předpokládejte, že nad povrchem hvězdy, který září jako černé těleso
o teplotě
![]() se nachází vrstva s optickou hloubkou
se nachází vrstva s optickou hloubkou
![]() ve stavu lokální termodynamické
rovnováhy. V pozorované oblasti spektra hvězdy se nachází atomární čára,
která má střed na vlnové délce
ve stavu lokální termodynamické
rovnováhy. V pozorované oblasti spektra hvězdy se nachází atomární čára,
která má střed na vlnové délce
![]() . S využitím výsledku
předcházejícího příkladu vypočtěte pozorovanou relativní intenzitu
v závislosti na vlnové délce (vyjádřené v násobcích Dopplerovské
šířky čáry
. S využitím výsledku
předcházejícího příkladu vypočtěte pozorovanou relativní intenzitu
v závislosti na vlnové délce (vyjádřené v násobcích Dopplerovské
šířky čáry
![]() ) v případě, že teplota vrstvy je
a)
) v případě, že teplota vrstvy je
a)
![]() , b)
, b)
![]() , c)
, c) ![]() . Přitom
položte zdrojovou funkci
. Přitom
položte zdrojovou funkci
![]() , kde
, kde ![]() je
tzv. Voigtova funkce s parametry
je
tzv. Voigtova funkce s parametry
![]() a
parametrem
a
parametrem ![]() , charakterizujícím Lorentzovské rozšíření čáry (zvolte
např.
, charakterizujícím Lorentzovské rozšíření čáry (zvolte
např. ![]() ). Voigtovu funkci aproximujte vztahem
). Voigtovu funkci aproximujte vztahem
![]() . Vysvětlete získané výsledky.
. Vysvětlete získané výsledky.
Řešení: Pro intenzitu záření černého tělesa je možné odvodit vztah
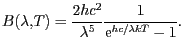
program prof;
const a=1.0;
tau0=1.0;
ts=5780.0;
tl=5000.0;
lam0=5000.0e-10;
var i,j:integer;
i0,u:double;
function voigt(v,agam:double):double; {Voigtova funkce}
begin
if(abs(v)>8.0) then
voigt:=agam/sqrt(pi)/(agam*agam+v*v)/sqrt(pi)
else
voigt:=(exp(-v*v)+agam/sqrt(pi)/(agam*agam+v*v))/sqrt(pi);
end;
function b(tep,lam:double):double;
const h=6.6256e-34; {Planckova konstanta}
c=2.99792e8; {rychlost svetla}
bolk=1.38054e-23; {Boltzmannova konstanta}
var lam5:double;
begin
lam5:=lam*lam*lam*lam*lam;
b:=2.0*h*c*c/lam5/(exp(h*c/lam/bolk/tep)-1.0);
end;
function profil(a,tau0,u:double):double;
var tau: double;
begin
tau:=tau0*voigt(u,a);
profil:=b(ts,lam0)*exp(-tau)+b(tl,lam0)*(1.0-exp(-tau));
end;
begin
u:=-10.0;
i0:=profil(a,tau0,u);
for i:=0 to 2000 do
begin
u:=u+0.01;
writeln(u,profil(a,tau0,u)/i0);
end;
end.
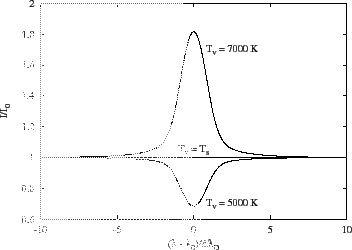
|
Na obrázku 10 jsou nakresleny profily čar, získané uvedeným programem. Jednotlivým případům uvedeným v zadání se budeme věnovat podrobněji. Obecně však platí (viz. výsledek předcházejícího příkladu 16), že v centru čáry, kde je optická hloubka vrstvy vysoká, se pozorovaná intenzita blíží Planckově funkci s teplotou rovnou teplotě vrstvy. Naopak v křídlech čáry, kde je optická hloubka vrstvy nízká, se pozorovaná intenzita blíží Planckově funkci s teplotou rovnou teplotě dopadajícího záření. Tento poznatek je také klíčem k pochopení jednotlivých případů. V případě a), kdy je teplota vrstvy nižší než teplota dopadajícího záření, je také hodnota Planckovy funkce v centru čáry nižší, než hodnota Planckovy funkce dopadajícího záření a my pozorujeme absorpční čáry. Tento model je možné použít pro vysvětlení vzniku absorpčních čar např. ve viditelném spektru Slunce. Opačný jev nastává v případě b), kdy je teplota vrstvy vyšší než teplota dopadajícího záření. Tento model popisuje vznik emisních čar. V případě c), kdy je teplota vrstvy rovna teplotě dopadajícího záření se vrstva spolu s okolním zářením nachází ve stavu termodynamické rovnováhy a žádné čáry nepozorujeme.
Úloha 14.18
Pro situaci popsanou v předcházejícím příkladě nakreslete závislost
ekvivalentní šířky čáry na optické hloubce čáry.
Řešení: Pro výpočet ekvivalentní šířky čáry v závislosti na její optické hloubce, je možné využít následující program:
program krivrust;
const taumin=0.5;
taumax=100.0;
ntau=300;
nlam=200;
u0=-800.0;
a=1.0;
ts=5780.0;
tl=5000.0;
lam0=5000.0e-10;
var x,gam: double;
i,j:integer;
tau0,w,it,i0,u,dltau,dlam:double;
begin
tau0:=taumin;
dltau:=exp((ln(taumax)-ln(taumin))/(ntau-1));
dlam:=2.0*abs(u0)/nlam;
for j:=0 to ntau do
begin
u:=u0;
i0:=profil(a,tau0,u);
w:=0;
for i:=0 to nlam do
begin
it:=(i0-profil(a,tau0,u))/i0;
u:=u+dlam;
if(i>0) and (i<nlam) then
w:=w+it
else
w:=w+0.5*it;
end;
w:=w*dlam;
writeln(tau0,' ',w);
tau0:=tau0*dltau;
end;
end.
Funkce voigt, b a profil zde nevypisujeme, všechny je možné převzít z předcházející úlohy 16. Graf, který byl získán uvedeným programem, je na obr. 11.
Úloha 14.19
Hvězdy s hmotnostmi
![]() a
a
![]() obíhají po kruhových drahách kolem společného hmotného
středu. Součet poloos
obou drah je
obíhají po kruhových drahách kolem společného hmotného
středu. Součet poloos
obou drah je
![]() , inklinační úhel
, inklinační úhel ![]() . Nakreslete
křivku radiálních rychlostí.
. Nakreslete
křivku radiálních rychlostí.
Řešení: Vzájemná rychlost obou hvězd je dána vztahem
program radrych;
const au=1.496e11;
ms=1.989e30;
a=2.0*au;
m1=0.5*ms;
m2=2.0*ms;
i=pi/6.0;
ntheta=1000;
g=6.67e-11;
rok=60.0*60.0*24.0*365.0;
var si,theta,v,v1,v2,mu,p,t:double;
j:integer;
begin
si:=sin(i);
mu:=m1*m2/(m1+m2);
p:=2.0*pi*sqrt(a*a*a/g/(m1+m2));
for j:=0 to ntheta do
begin
theta:=2.0*pi*j/ntheta;
v:=sqrt(g*(m1+m2)/a);
v1:=-v*mu/m1*sin(theta)*si;
v2:=v*mu/m2*sin(theta)*si;
t:=j/ntheta*p/rok;
writeln(t,' ',v1,' ',v2);
end;
end.
Úloha 14.20Nakreslete graf Rocheova potenciálu v rovině oběhu složek
pro dvojhvězdu s hmotností složek
![]() ,
,
![]() se vzdáleností středů hvězd
se vzdáleností středů hvězd ![]() . Na
základě výsledků diskutujte povahu Lagrangeových bodů.
. Na
základě výsledků diskutujte povahu Lagrangeových bodů.
Řešení: Potenciál
m1=0.85 m2=0.17 x1=m2/(m1+m2) x2=m1/(m1+m2) mcos(a,b)=a/b r1(x,y)=(x1*x1+x*x+y*y+2*x1*(x*x+y*y)**0.5*mcos(x,(x*x+y*y)**0.5))**0.5 r2(x,y)=(x2*x2+x*x+y*y-2*x2*(x*x+y*y)**0.5*mcos(x,(x*x+y*y)**0.5))**0.5 splot -(m1/r1(x,y)+m2/r2(x,y)+0.5*(m1+m2)*(x*x+y*y))/(m1+m2)

|
Výsledek je na obrázku 13. Lagrangeovy body ![]() ,
, ![]() a
a ![]() jsou sedlovými body potenciálu, v Lagrangeových
bodech
jsou sedlovými body potenciálu, v Lagrangeových
bodech ![]() a
a ![]() dosahuje potenciál svého maxima.
dosahuje potenciál svého maxima.
Úloha 14.21
V případě, že v dvojhvězdě přetéká hmota, je možné rychlost přenosu
odhadnout vztahem
![]() , kde
, kde ![]() je hustota látky která
přetéká z hvězdy o poloměru
je hustota látky která
přetéká z hvězdy o poloměru ![]() na druhou hvězdu průřezem o ploše
na druhou hvězdu průřezem o ploše ![]() .
Odhadneme-li plochu jako
.
Odhadneme-li plochu jako
![]() , kde
, kde ![]() je tloušťka vrstvy, která
přesahuje Rocheovu plochu a rychlost
je tloušťka vrstvy, která
přesahuje Rocheovu plochu a rychlost ![]() položíme rovnu tepelné rychlosti,
pak rychlost přenosu hmoty je možné odhadnout
položíme rovnu tepelné rychlosti,
pak rychlost přenosu hmoty je možné odhadnout
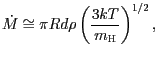
Řešení: Pro výpočet závislosti rychlosti přenosu hmoty
program phmot;
const rhv=7.11e8; {polomer hvezdy}
rcgs=0.01; {prepocet CGS}
rhocgs=1000.0; {prepocet CGS}
ms=1.989e30; {hmotnost Slunce}
bolk=1.38054e-23; {Boltzmannova konstanta}
mh=1.6735e-27; {hmotnost atomu vodiku}
var dm,r,qm,lr,t,p,rho: double;
i: integer;
begin
for i:=1 to 424 do
begin
readln(r,qm,lr,t,p,rho);
dm:=pi*rhv*(rhv-r*rcgs)*rho*rhocgs*sqrt(3.0*bolk*t/mh);
writeln(1.0-r*rcgs/rhv,dm/ms);
end;
end.
Úloha 14.22Zjistěte periodu hvězdy CQ UMa.
Řešení: Na adrese http://adsabs.harvard.edu zvolíme "Search", "Astronomy and Astrophysics Search" a jako "Object name" zadáme "CQ UMa". Zvolíme hledání, "Send Query". Podle názvu zvolíme článek, který se týká hledání periody, získáme jeho pdf verzi a vyhledáme určenou periodu. Například v článku Improvement of the Period of CQ UMa autorů Jozefa Žižňovského a Zdeňka Mikuláška (IBVS, číslo 4259, strana 1) nalezneme periodu
Úloha 14.23Nakreslete světelnou křivku zákrytové dvojhvězdy GG Lup.
Řešení: Na adrese http://cds.u-strasbg.fr zvolíme "Catalogs", zadáme hledání
Úloha 14.24 Pro teplotu akrečního disku platí vztah
![$\displaystyle T=\left(\frac{3GM\dot{M}}{8\pi\sigma R_{S}^{3}}\right)^{1/4}
\le...
...frac{R_S}{r}\right)^{3/4}\left[1-\left(\frac{R_S}{r}\right)^{1/2}\right]^{1/4}.$](dimg2801.gif)
Řešení: Pro získání grafů 16 a 17 je možné použít následující program:
program disk;
const ms=1.989e30; {hmotnost Slunce}
m=3.82*ms;
g=6.67e-11; {gravitacni konstanta}
dmdt=1.0d14;
sig=5.67051d-8; {konstanta Stefan-Boltzmannova zakona}
c=2.99792e8; {rychlost svetla}
b=0.0029; {konstanta Wienova zakona}
var rs,tdisk,r,dr,ddr,t,mlam: double;
i: integer;
begin
rs:=2.0*g*m/c/c;
tdisk:=3.0*g*m*dmdt/8.0/pi/sig/rs/rs/rs;
tdisk:=sqrt(sqrt(tdisk));
r:=3.0*rs;
for i:=1 to 500 do
begin
r:=1.015*r;
dr:=sqrt(rs/r);
ddr:=sqrt(dr);
t:=tdisk*ddr*ddr*ddr*sqrt(sqrt(1.0-dr));
mlam:=b/t;
writeln(r/rs,t,mlam*1.0e9);
end;
end.
4mm
Úloha 14.25S pomocí katalogu TYCHO nakreslete histogram počtu hvězd na obloze podle
jejich pozorované hvězdné velikosti. Předpokládejte, že jsou hvězdy v prostoru rozloženy
rovnoměrně a že všechny hvězdy mají stejnou hvězdnou velikost. Spočtěte za
těchto předpokladů rozdělovací funkci hvězd podle jejich hvězdné velikosti a
porovnejte se získaným histogramem. Co můžeme na základě těchto úvah usuzovat o
mezihvězdné extinkci?
Řešení: Na stránce CDS http://cdsweb.u-strasbg.fr/cats/Cats.htx, na které je možné hledat astronomické katalogy, zadáme hledání "TYCHO". Zvolíme "I/197A Tycho Input Catalogue, Revised version (Egret+ 1992)", ("VizieR query form"). Pro úsporný výpis zvolíme "Maximum Entries per table" jako "unlimited", "Output layout" jako "tiny ascii" a zaškrtneme výpis pouze položky "Vmag". Jako kritérium pro hledání zadáváme např. "4+/-0.5" (postupujeme např. po celých magnitudách). Na základě počtu nalezených hvězd získáme následující obrázek 18.
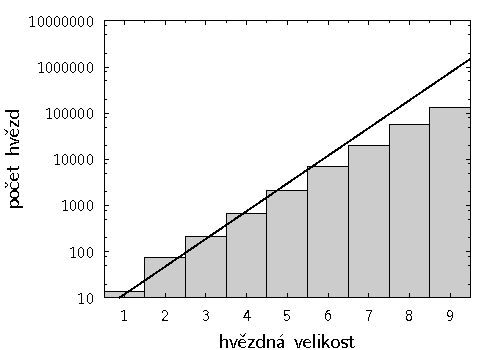
|
Počet hvězd ![]() v kouli o poloměru
v kouli o poloměru ![]() je úměrný
je úměrný ![]() . Vzdálenost, do
které uvidíme hvězdy hvězdné velikosti
. Vzdálenost, do
které uvidíme hvězdy hvězdné velikosti ![]() , které mají stejnou absolutní
hvězdnou velikost
, které mají stejnou absolutní
hvězdnou velikost ![]() je dána vztahem
je dána vztahem
![]() , kde
, kde ![]() je vyjádřeno
v parsecích. Počet hvězd je tedy úměrný
je vyjádřeno
v parsecích. Počet hvězd je tedy úměrný
![]() , počet hvězd
s danou hvězdnou velikostí je úměrný
, počet hvězd
s danou hvězdnou velikostí je úměrný
![]() . Tato křivka je
nakreslena nepřerušovanou čarou v obrázku 18. Slabých hvězd
pozorujeme nápadně méně, než by to odpovídalo uvažovanému modelu, důvodem je
vliv mezihvězdné extinkce.
. Tato křivka je
nakreslena nepřerušovanou čarou v obrázku 18. Slabých hvězd
pozorujeme nápadně méně, než by to odpovídalo uvažovanému modelu, důvodem je
vliv mezihvězdné extinkce.
Úloha 14.26
Určete zářivý výkon aktivní galaxie Cygnus A v rádiovém oboru pomocí
zářivého toku uvedeného v tabulce, víte-li, že galaxie je vzdálena
![]() .
.
|
|
|
|||
|
|
[
|
|
[
|
|
Řešení: Abychom získali zářivý výkon v radiovém oboru, musíme integrovat zářivý tok přes všechny frekvence a sečíst tok na kouli o poloměru
program agn;
const nf=10;
d=250.0;
mpc=3.09e22;
var nu,nus,f,fs,lr,r: double;
i: integer;
function des(x: double) : double;
begin
des:=exp(x*ln(10.0));
end;
begin
lr:=0.0;
for i:=1 to nf do
begin
read(nu,f);
nu:=des(nu);
f:=des(f);
if(i > 0) then lr:=lr+0.5*(fs+f)*(nu-nus);
fs:=f;
nus:=nu;
end;
r:=d*mpc;
lr:=4.0*pi*r*r*lr;
writeln(lr);
end.
Zářivý výkon galaxie Cygnus A v rádiovém oboru je
Úloha 14.27Nalezněte článek autorů Penziase a Wilsona, za který jim byla udělena
Nobelova cena.
Řešení: Na adrese http://adsabs.harvard.edu zvolíme "Search", "Astronomy and Astrophysics Search" a jako autory (na každý řádek jednoho) napíšeme Penzias a Wilson, zaškrtněte AND, klepneme na "Send Query". Hledaným článkem je A Measurement of Excess Antenna Temperature at 4080 Mc/s (Astrophysical Journal, číslo 142, strana 419). Kliknutím na odkaz vybraného článku pak získáte jeho abstrakt, je možné získat přímo samotný článek.
Úloha 14.28Pomocí vzáleností galaxií a jejich radiálních galaxií uvedených v článku
W. A. Freedman a kol., Astrophysical Journal, číslo 553, strana 47,
spočtěte hodnotu Hubbleovy konstanty.
Řešení: Článek získáme například na adrese http://adsabs.harvard.edu. Z tabulky 4 tohoto článku převezmeme vzdálenosti galaxií
Jiri Krticka