CD - Hydrodynamika obálek horkých hvězd

Kelvinova-Helmholtzova nestabilita

Kelvinova-Helmholtzova nestabilita je klasickým jednoduchým příkladem nestabilního chování tekutiny. Lze na ní názorně demonstrovat, jak v relativně jednoduchém případě vedou hydrodynamické rovnice k nestabilnímu chovaní. Projevuje se v případě, kdy jsou rozdílné vrstvy tekutiny vůči sobě v relativním pohybu. Matematickou analýzu Kelvinovy-Helmholtzovy nestability provedl Helmholtz v roce 1886. Zkoumal případ dvou vrstev v tekutině s různou hustotou, které se vuči sobě pohybovaly. S Kelvinovou-Helmholtzovou nestabilitou můžeme často setkat v astrofyzikálních aplikacích. Namátkou lze uvést pozorované struktury extragalaktických jetů (Birkinshaw, 1991).

Jako model jsem zvolil kontinuum, horizontálně rozdělené na dvě vrstvy s odlišnou hustotou. Horní vrstva má menší hustotu než spodní vrtsva a vůči spodní vrstvě se pohybuje proti směru osy x. Na začátku jsem na hranici obou vrstev vytvořil malou poruchu v podobě harmonické vlny. Detailní specifikace problému, včetně matematické analýzy problému je uvedena v disertační práci na straně 24 až 28.

Animace Kelvinovy-Helmholtzovy nestability

Simulaci jsem provedl pomocí hydrodynamického kódu VH-1 (viz. dodatek D v disertační práci). V rámci dobrého rozlišení jednotlivých fází nestability jsem numerické výpočty prováděl v prostorové síti 600x600 bodů. Pro x-ové okraje jsem zvolil pevné okrajové podmínky, zatímco pro y-ové okraje jsem zvolil periodické okrajové podmínky. Počáteční podmínky a velikost barevné škály je uvedena v disertační práci v dodatku D.

Rayleighova-Taylorova nestabilita

Rayleighova-Taylorova nestabilita je druhým názorným příkladem nestabilního chování tekutiny. Poprvé byla objevena a popsána lordem Rayleighem v roce 1880, který pozoroval chování dvou tekutin s různou hustotou v gravitačním poli. Později byla v zobecněné formě rozpracována sirem Geoffrey Taylorem v roce 1950. Po nich také tato nestabilita nese svůj název. Patří mezi jednu z nejznámějších nestabilit v klasické hydrodynamice. Obecně se uplatňuje tehdy, pokud je hustší kontinuum urychlováno skrze kontinuum s menší hustotou, což je situace, která se velmi často vyskytuje v astrofyzikálních aplikacích, například při výbuchu supernovy (Dwarkadas, 2000). S tímto typem nestability se můžeme i setkat ve hvězdném větru (Nelson et al.), kde se kombinuje se zářivou nestabilitou (viz disertační práce, strana 65 - 68). Často se můžeme setkat s případem, kdy se obě nestability, tedy Kelvinova-Helmholtzova nestability a Rayleighova-Taylorova nestabilita kombinují.

Jako model jsem opět zvolil kontinuum horizontálně rozdělené na dvě vrstvy s odlišnou hustotou. Horní vrstva má hustotu větší než spodní vrtsva, přičemž obě dvě vrstvy jsou na počátku v klidu. Gravitační zrychlení má vertikální směr a míří se shora dolů. Opět jsem na začátku simulace vytvořil na hranici obou vrstev poruchu v podobě harmonické vlny. Detailní specifikace problému, včetně matematické analýzy problému je uvedena v disertační práci na straně 19 až 24.

Animace Rayleighovy-Taylorovy nestability

Simulaci jsem provedl pomocí hydrodynamického kódu VH-1 (viz. dodatek D v disertační práci). V rámci dobrého rozlišení jednotlivých fází nestability jsem výpočty prováděl v prostorové síti 600x600 bodů. Pro x-ové okraje jsem opět zvolil pevné okrajové podmínky, zatímco pro y-ové okraje jsem zvolil periodické okrajové podmínky. Počáteční podmínky a velikost barevné škály je uvedena v disertační práci v dodatku D.

Rázová vlna ve hvězdném větru

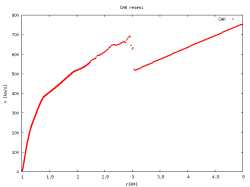
Pokud simulujeme hvězdný vítr horkých hvězd v jednosložkové aproximaci s počátečními podmínkami, které se výrazně liší od stacionárního řešení, dochází ke vzniku rázové vlny. Stacionární řešení jednosložkového modelu hvězdného větru se zářivou silou v Sobolevově aproximaci je popsáno CAK řešením a reprezentuje určitý typ atraktoru. Detailní popis vzniku rázových vln při numerické simulaci CAK řešení hvězdného větru hydrodynamickým kódem s časovým průběhem je v disertační práci na straně 66.

Numerické simulace byly prováděny pomocí hydrodynamického kódu flu.f. Pro model jsem použil parametry odpovídající hvězdě &kappa Cas (viz tabulka 7.2 v disertační práci). Simulace byla provedena na prostorové síti 900 prostorových bodů rovnoměrně pokrývajících oblast 5R* (hvězdných poloměrů). Okrajové podmínky byly nastaveny v souladu s charakteristikami systému, na vnitřním okraji jsem extrapoloval tok a nastavil konstantní hustotu. Na vnějším okraji jsem obě veličiny, tedy tok i hustotu extrapoloval. Další detaily ohledně výpočtu, konkrétně počáteční podmínky, hodnoty Courantova čísla a dalších parametrů lze nalézt na straně 66.

Vznik rázové vlny

Při přechodu ze zvolených počátečních podmínek do stacionárního řešení vzniká rázová vlna. Po jejím odeznění již hvězdný vítr pokračuje v přechodu na CAK řešení spojitě. Po skončení simulace modelované řešení věrně koresponduje s CAK řešením. Rázová vlna tedy nepopisuje realný fyzikální děj, ale spíše ukazuje, jak moc se zvolené počáteční podmínky odlišují od reálného průběhu. Zajímavé je, že při simulacích vícesložkového hvězdného větru již k tomuto artefaktu nedochází, zjevně důsledkem tlumícího efektu třecí síly.

Pulsující obálky

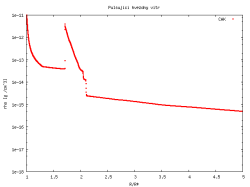
Zajímavý jev nastává, pokud zářivou sílu od určité vzdálenosti, kde je lokální rychlost kontinua menší než úniková rychlost, položíme rovnu nule. Tento model zjednodušeně popisuje situaci, která může nastat při vícesložkovém popisu hvězdného větru. Ve dvousložkovém hvězdném větru je zářením urychlována pouze část plazmatu (aktivní složka), zatímco druhá část plazmatu se zářením neinteraguje (pasivní složka). Aktivní složka předává část své hybnosti skrze coulombické interakce pasivní složce. Za určitých podmínek přestává být mechanismus zajišťující přenos hybnosti mezi aktivní složkou a pasivní složkou efektivní a dochází k oddělení obou složek. Pokud k tomuto oddělení dojde v místě, kde je lokální rychlost menší než úniková, pak popsaná situace odpovídá našemu zjednodušenému modelu.

Numerické simulace byly prováděny pomocí hydrodynamického kódu flu.f. Pro modelovou hvězdu jsem použil parametry odpovídající hvězdě &epsilon Ori (viz tabulka 7.2 v disertační práci). Simulace byla provedena v prostorové síti 900 prostorových bodů, rovnoměrně pokrývajících oblast 5R* (hvězdných poloměrů). Okrajové podmínky byly nastaveny v souladu s charakteristikami systému, na vnitřním okraji jsem extrapoloval tok a nastavil konstantní hustotu. Na vnějším okraji jsem extrapoloval obě veličiny. Tyto okrajové podmínky však neplatili vždy. Pokud byla rychlost (tedy i tok) na vnějším okraji záporná, zafixoval jsem rychlost na vnějším okraji na nule a hustotu na velmi malou hodnotu. Detailně je tato úprava okrajových podmínek diskutována v disertační práci na straně 67. Zářivou sílu jsem vynuloval od vzdálenosti r=1.2R*, kde platí podmínka, že lokální rychlost na tomto místě je menší než rychlost úniková. Další detaily ohledně výpočtu, konkrétně počáteční podmínky, hodnoty Courantova čísla a dalších parametrů lze nalézt na straně 66.

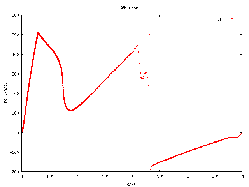Jak je patrné z animace, nejprve se v určité vzdálenosti od hvězdy vytvoří hustá obálka, která na cestě zpět k povrchu hvězdy interaguje s hvězdným větrem od hvězdy. Jak postupně obálka padá, získává více a více hmoty a tak padá k povrchu hvězdy rychleji a rychleji. Po kontaku obálky s hvězdou může hvězdný vítr opět volně expandovat, přičemž s sebou posbírává část materiálu z předchozího cyklu, který nedopadl na hvězdu. Začíná se tak tvořit další obálka. V okamžiku, kdy hmota zase padá zpět se celý cyklus opakuje. Vytváří se pravidelně pulsující obálka s periodou zhruba zhruba 59 hodin. Odkazy na literaturu a detailní technický popis simulace lze nalézt na straně 66, 67, 70 a 71 v disertační práci.

Vícesložkový hvězdný vítr

Vlastní vyvinutý hydrodynamický kód pro vícesložkové simulace hvězdného větru mflu.f jsem testoval na hvězdách z tabulky 7.2. v disertační práci. V této tabulce jsou také shrnuty jejich fyzikální parametry. Konkrétně jsem se zabýval hvězdami s parametry hvězd &epsilon Ori, &kappa Cas, &tau Sco a &epsilon Per. U těchto hvězd se potvrdil předpoklad dobře vázaného hvězdného větru.

CAK řešení pro vícesložkový hvězdný vítr

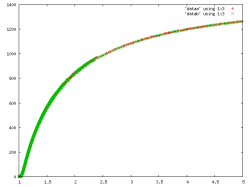Pro simulaci jsem použil vícesložkový kód mflu.f. Detailní popis kódu včetně použité metody pro výpočet dynamického tření je v sekci 7.4 disertační práce. Jako modelový příklad pro animaci jsem vybral hvězdu s parametry &epsilon Ori. V rámci dobrého rozlišení jsem pro výpočet použil prostorovou síť 1600 prostorových bodů rovnoměrně pokrývajících oblast 5R* (hvězdných poloměrů). Další detaily ohledně výpočtu, konkrétně počáteční podmínky, hodnoty Courantova čísla a dalších parametrů lze nalézt na straně 89 až 101 disertační práce. U dobře vázaného hvězdného větru vícesložkové simulace vykazují dobrou shodu v porovnání s jednosložkovými modely. Také se ukázalo, že pro tyto hvězdy metoda dobře konverguje i pro horší aproximace Chandrasekharovy funkce (detaily viz sekce 7.6).